强化学习基础概念

State ：观测到的环境状态
Action ：当前 Agent 选择的行为
Policy ： Agent 选择行为的依据的策略
Reward ：执行完 Action 之后得到的激励
State’ ：执行完策略之后环境状态

强化学习流程

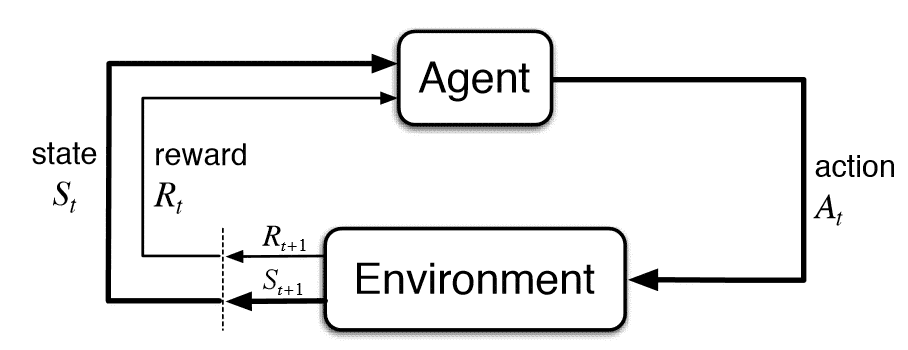
Q-learning 算法概述

奖励矩阵 $R_{s,a}$ ：表示在 $s$ 状态下采取动作 $a$ 时，从环境中获得的即时奖励 Reward
Q 值矩阵 $Q_{s,a}$ ：表示从 $s$ 状态下采取动作 $a$ 时，并在未来遵循最佳策略所能获得的累计奖励的估计
- 初始化为 0 矩阵
核心思想：不断更新 Q 值矩阵 $Q_{s,a}$ 来逼近最优 Q 值矩阵‘，从而得到所谓的最优策略
更新公式：$Q(s, a) \leftarrow Q(s, a) + \alpha \left[ R + \gamma \max_{a’} Q(s’, a’) - Q(s, a) \right]$
训练过程：
- 给定 $\gamma$ 和 reward 矩阵 $R_{s,a}$ ；
- 初始化 Q 值矩阵 $Q_{s,a}$ 为零矩阵；
- For each episode：
  - 随机选择一个初始状态 State；
  - 执行以下步骤直到达到目标状态
    - 在当前状态 $s$ 的所有可能行为中选取一个行为 $a$；
    - 利用选定的行为 $a$ , 得到下一个状态 $\tilde{s}$；
    - 按照公式，计算 $Q(s,a)$；
    - 令 $s=\tilde s$ 。
推理过程：
- 令当前状态 $s=s_0$ ；
- 确定 $a$ , 它满足 $Q(s,a)=max_{\tilde a}{Q(s,\tilde a)}$ ；
- 令当前状态 $s =\tilde s$ （ $\tilde s$ 表示 $a$ 对应的下一个状态 )；
- 重复执行上述两步直到成为目标状态。

代码举例

import numpy as np

# 定义参数
gamma = 0.8  # 折扣因子
alpha = 0.1  # 学习率
epsilon = 0.1  # 探索概率
episodes = 10000  # 学习的总回合数

# 定义收益矩阵
R = np.array([
    [-1, -1, -1, -1, 0, -1],
    [-1, -1, -1, 0, -1, 100],
    [-1, -1, -1, 0, -1, -1],
    [-1, 0, 0, -1, 0, -1],
    [0, -1, -1, 0, -1, 100],
    [-1, 0, -1, -1, 0, 100]
])

# 初始化Q值矩阵
Q = np.zeros_like(R, dtype=float)

# Q-learning算法
for episode in range(episodes):
    # 随机选择初始状态
    state = np.random.randint(0, R.shape[0]) # 
    
    while True:
        # 选择动作：采用ε-贪婪策略
        if np.random.rand() < epsilon:
            action = np.random.randint(0, R.shape[1])
        else:
            action = np.argmax(Q[state])

        # 执行动作，获取即时奖励和下一个状态
        next_state = action
        reward = R[state, action]
        
        # 只在奖励不为 -1 时进行 Q 值更新
        if reward != -1:
            # Q值更新
            Q[state, action] = Q[state, action] + alpha * (reward + gamma * np.max(Q[next_state]) - Q[state, action])

            # 状态转移
            state = next_state
        
        # 如果达到了终止状态，结束本回合
        if reward == 100:
            break

# 对 Q 矩阵进行规范化，使最大值为100
max_value = np.max(Q)
if max_value > 0:
    Q = (Q / max_value) * 100

# 保留两位小数
Q = np.round(Q, 2)

# 输出最终的Q值矩阵
print("最终的Q值矩阵（规范化后）：")
print(Q)

# 输出最终策略
policy = np.argmax(Q, axis=1)
print("最终策略：")
print(policy)

# 解释最终策略
for state in range(len(policy)):
    print(f"在状态 {state} 下，选择动作 {policy[state]} 作为最优策略。")

总结

Q-learning 的 reward 作为学习的监督， Q 值矩阵作为学习到的知识， Q 值矩阵的更新过程需要借助还未更新的下一状态的最大 Q 值或 $\varepsilon$ 控制的随机 Q 值。

强化学习基础概念

强化学习流程

Q-learning 算法概述

代码举例

总结

参考文章