电机控制
为什么要写这个笔记?本人基础很菜,看书痛苦不堪,但更不喜欢听课,网上资料难得,所以想要记录下自己学习本课程时,从一个菜狗逐步摸索的过程
本笔记的思路借鉴于OSTEP,希望呈现出一个渐进的过程,而不是直说结论;致敬OSTEP,如果每本教材都能有如此质量,你会觉得知识很简单
为什么只有两章?因为后面的我还没学
声明:
- 我不能完全保证正确,因为我是菜狗
- 我的符号可能和教材不一样,因为我感觉教材的符号标的不好
- 简单的图片我希望自己画,但是太耗时间,只能拍书上的照片
- 考试出分:期末考了
60+,说实话超出我的预期,我的目标是不挂科的,毕竟只是考试前突击了下(需要一个好老师,不那么在乎课堂表现;需要一个hxd教你怎么做实验、写报告)
第二章电机负载系统基础
电机负载系统的动力学方程
先推导单轴系统,再推导多轴系统到单轴系统的等效
以下图为例, $T_e$ 为电机给传动轴的电磁转矩, $T_L$ 为负载给传动轴的负载转矩, $n$ 为转速,则转动角速度 $\Omega = \frac{2\pi n}{60}$
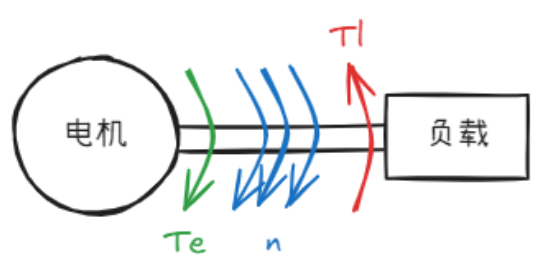
由转动定律可得 $T_e - T_L = J\frac{d\Omega}{dt}=J\frac{2\pi}{60}\frac{dn}{dt}$
$J=\frac{GD^2}{4g}$ , $\pi$ 取 $3.14$ 后近似处理
则最终的动力学方程为 $T_e - T_L = \frac{GD^2}{375}\frac{dn}{dt}$
上述方法没有考虑多个轴的情况,下图是一种多轴系统举例,将以此来说明多轴等效到单轴
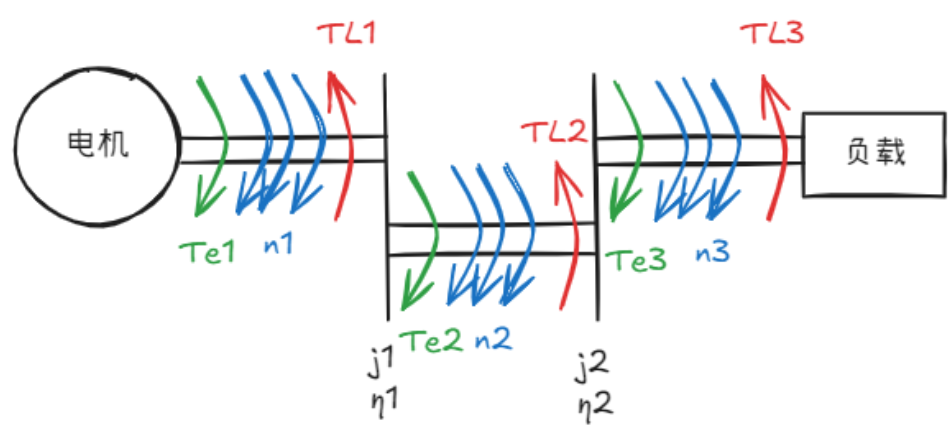
首先解释下图中的变量名
- $T_{e1}$ 为第一段的电机给传动轴的电磁转矩, $T_{e2}$ 和 $T_{e3}$ 虽不是电磁转矩,但为了统一,还是这样记录
- $T_{L1}$ 、 $T_{L2}$ 、 $T_{L3}$ 分别为三段的负载转矩
- $n_1$ 、 $n_2$ 、 $n_3$ 分别为三段的转速
- $j_1$ 为一段到二段齿轮比,则 $j_1 = \frac{n_1}{n_2}$ , $j_2$ 同理,则有 $j_2 = \frac{n_2}{n_3}$
- $\eta _1$ 为一段到二段的效率, $\eta_2$ 同理
我们规定等效时,满足从电机侧看过去的情况不变,即 $T_{e1}$ 为等效后的 $T_{e}$ ,转速 $n_1$ 为等效后的 $n$
因为要研究电机控制——等效到电动机的轴上
- 折算前后要满足功率不变
- $T_{L}\cdot\eta_1\cdot\eta_2\cdot n_1=T_{L3}\cdot n_3$
- 折算前后的系统存储的动能相同
- $\frac{1}{2}\frac{GD_L^2}{4g}\Omega^2=\frac{1}{2}\frac{GD_{L_1}^2}{4g}\Omega_1^2+\frac{1}{2}\frac{GD_{L_2}^2}{4g}\Omega_2^2+\frac{1}{2}\frac{GD_{L_3}^2}{4g}\Omega_3^2$
电机负载系统的负载特性
负载特性是负载转矩和转速的关系,转矩和转速均与功率有关
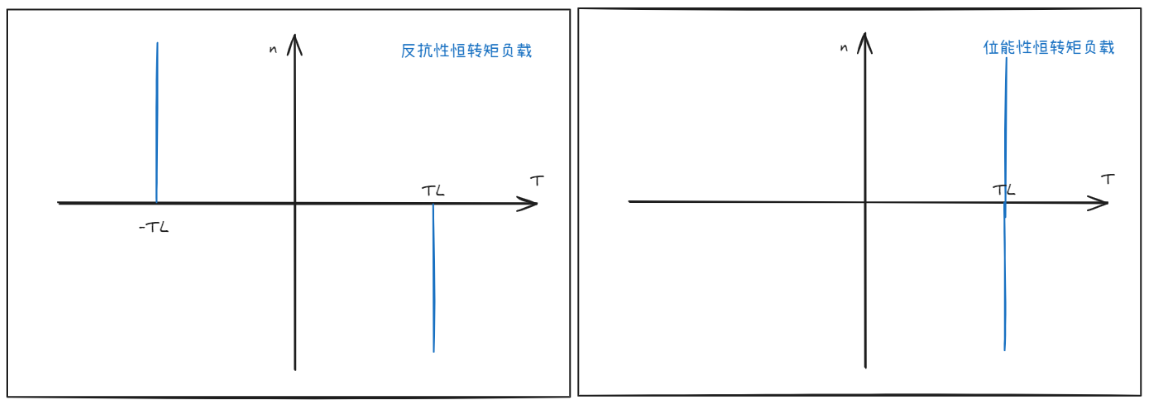
恒转矩负载,转速 $n$ 改变时,负载转矩 $T_L$ 恒定不变
- 反抗性恒转矩负载,转矩总是和转速方向相反,反抗运动的制动转矩
- 举例:摩擦负载
- 位能性恒转矩负载,转矩的方向不变
- 举例:电梯的负重提供的负载,方向始终是向下,电梯上行时,与转速方向相同,电梯下行时,与转速方向相反
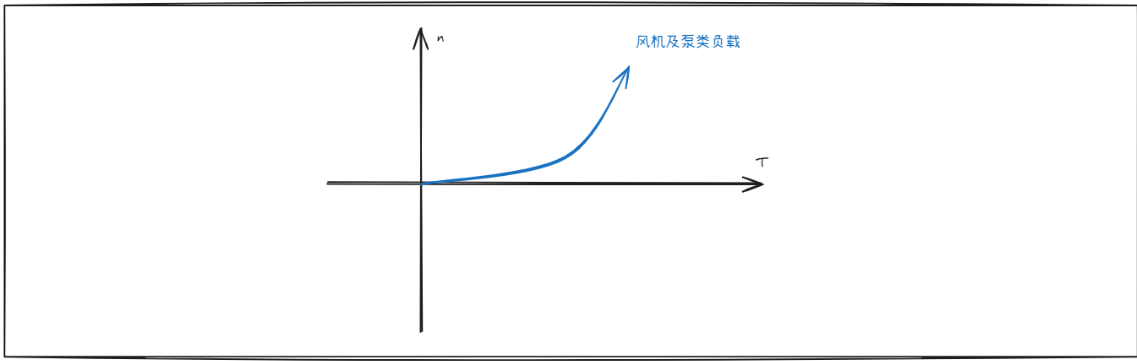
风机和泵类负载,负载转矩和转速平方成正比,即 $T_L=k\times n_L^2$
恒功率负载,转矩和转速成反比,即 $T_L n_L=k$
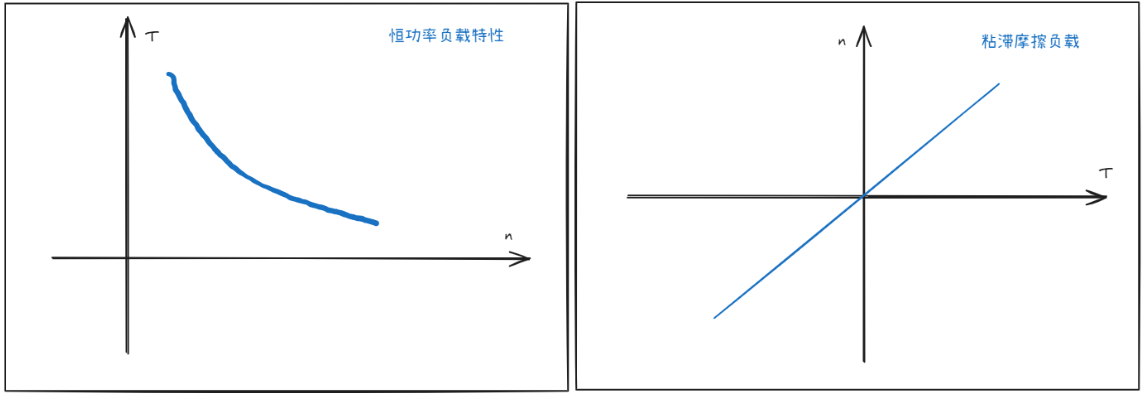
粘滞摩擦负载,转矩和转速成正比,即$n=k\times T_L$
电机负载系统稳定运行条件
电机的机械特性曲线和负载特性曲线图
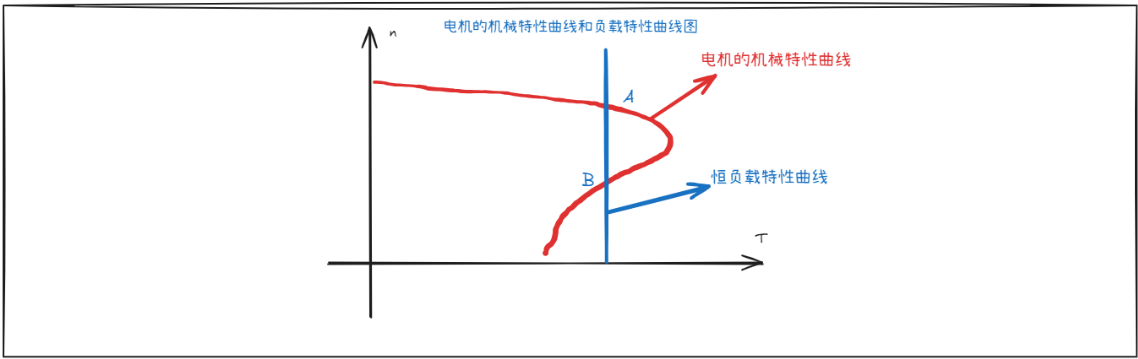
必要条件
$T_L=T_e$ ,转矩差为零,则转速的微分为 $0$ ,图中 A 、 B 两点均满足
充要条件
其中 A 点为稳定运行点,为什么? A 点负载转矩若因为扰动增大一点,则 $T_L>T_e$ ,转速会增大,而转速 $n$ 增大后,电磁转矩 $T_e$ 会增大,从而达到新的平衡;反之同理
B 点不满足上述分析,故不为稳定运行点
选择调速的基本依据
调速范围、负载能力、平滑性、经济性
第三章电机控制的核心
所有电机等效为直流电机进行控制
电机控制包括位置控制、速度控制、转矩控制
- 速度控制:调节电机的转速,使其达到设定值并保持稳定。
- 转矩控制:调节电机的输出转矩,以满足负载需求。
- 位置控制:精确控制电机转子的位置,常用于伺服系统。
机电能量
由单线圈励磁得到磁能与电感的关系
推广到双线圈励磁时有哪些变化
电机可看作双线圈,从而推导电磁转矩
单线圈励磁及磁能计算
求磁路欧姆定律
根据安培环路定理 ($\oint_L \vec H \cdot d \vec l=\Sigma i$) 可得, $H_ml_m+H_\delta\delta=N_Ai_A=f_A$ (磁动势)
考虑磁场强度和磁感应强度的关系, $f_{A}=\frac{B_{m}}{\mu_{\mathrm{Fe}}}l_{m}+\frac{B_{\delta}}{\mu_{\delta}}\delta$ ,并且磁通量是连续的,即 $B_m=B_\delta$
可得磁路欧姆定律, $f_{A}=(B_{m}S)\left(\frac{l_{m}}{\mu_{\mathrm{Fe}}S}\right)+(B_{m}S)\left(\frac{\delta}{\mu_{0}S}\right) = \varphi_{mA} (R_m + R_\delta)$
- $R_m=\frac{l_m}{\mu_{Fe}S}$ , $R_\delta=\frac{\delta}{\mu_0 S}$ , 定义 $R_{m\delta}=R_m+R_\delta$
求电感、磁链
定义线圈 A 的励磁磁链 $\psi_{mA}=N_A\varphi_{mA}$
代入 $f_A=\varphi_{mA}R_{m\delta}$ ,则励磁磁链 $\psi_{mA}=N_A\varphi_{mA}=N_A\frac{f_A}{R_{m\delta}}=N_A\frac{N_A i_A}{R_{m\delta}}=\frac{N_A^2}{R_{m\delta}}i_A$
电感的定义是 $L = \frac{\psi}{i}$ , 故可以得到,励磁电感 $L_{mA}=\frac{N_A^2}{R_{m\delta}}$
此外还有漏磁场(不是气隙、几乎为0),对应的漏电感$L_{\sigma A}$
则有自感$L_A=L_{mA}+L_{\sigma A}$
从而将线圈 A 产生磁链的能力表现为一个集中参数自感 $L_A$
线圈的自感磁链为 $\psi_A=L_Ai_A$
求磁能
根据电磁感应定律有 $e_A=-\frac{d\psi_A}{dt}$
$u_A=i_AR-e_A=i_AR+\frac{d\psi_A}{dt}$
$dt$ 时间流入磁场的能量,$dW_m=u_Ai_Adt-i_ARdt=i_Ad\psi_A$
若磁场能量不继续转化为机械能,则继续储存在磁场中
则磁场中存放的能量为$W_m=\int_0^{\psi_{mA}}i_Ad\psi_A$,将这部分能量称为磁能
这部分能量是纯流入磁场的能量
根据能量守恒定律,有 $W_{all}=W_m+W_{热}$
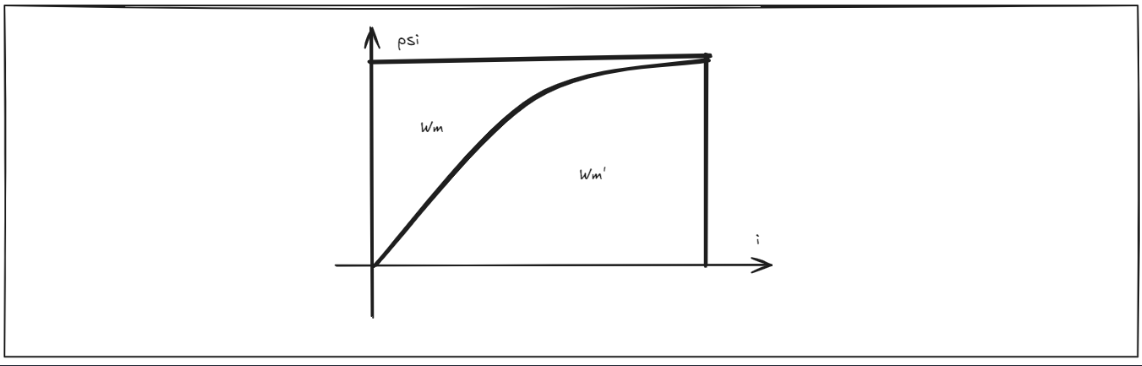
忽略铁心磁路的磁阻,则磁路的磁阻为气隙的磁阻,磁阻为定值,则励磁电感为定值, $\psi$ 和 $i$ 为线性关系,则有 $W_m=\frac{1}{2}L_{mA}i_A^2$
下图的 $W_m$ 部分为磁能,下方的 $W_m’$ 部分为磁共能(它不是实际存在的,而是为了求电磁转矩而假设出来的与 $W_m$ 同量纲的量)
双线圈励磁及磁能计算
考虑 A 、 B 两个线圈
- 线圈 B 的自感为 $L_B=L_{mB}+L_{\sigma B}$ ,同线圈 A
- 线圈 A 、 B 之间有交链的磁通,互感 $L_{AB}=L_{BA}=\frac{N_AN_B}{R_{m\delta}}$
- 线圈 A 的全磁链为 $\psi_A=L_Ai_A+L_{AB}i_B$
- 线圈 B 的全磁链为 $\psi_B=L_Bi_B+L_{BA}i_A$
- 则在 $dt$ 时间流入线圈 A 、 B 的净电能 $dW=i_Ad\psi_A+i_Bd\psi_B$
- 则磁场中存放的能量为 $W_m=\int_0^{\psi_{mA}}i_Ad\psi_A+\int_0^{\psi_{mB}}i_Bd\psi_B$ ,将这部分能量称为磁能
机电能量转换分析
对于只有两个线圈的情况
- 只改变电流 $i_A$ 和 $i_B$ 只能增加或减少磁场能量,电能无法转化为机械能,这是因为没有运动的部件
- 故需要转子的转动来沟通机械能和磁能(如下图,这个图太难画,直接拍老师的书)
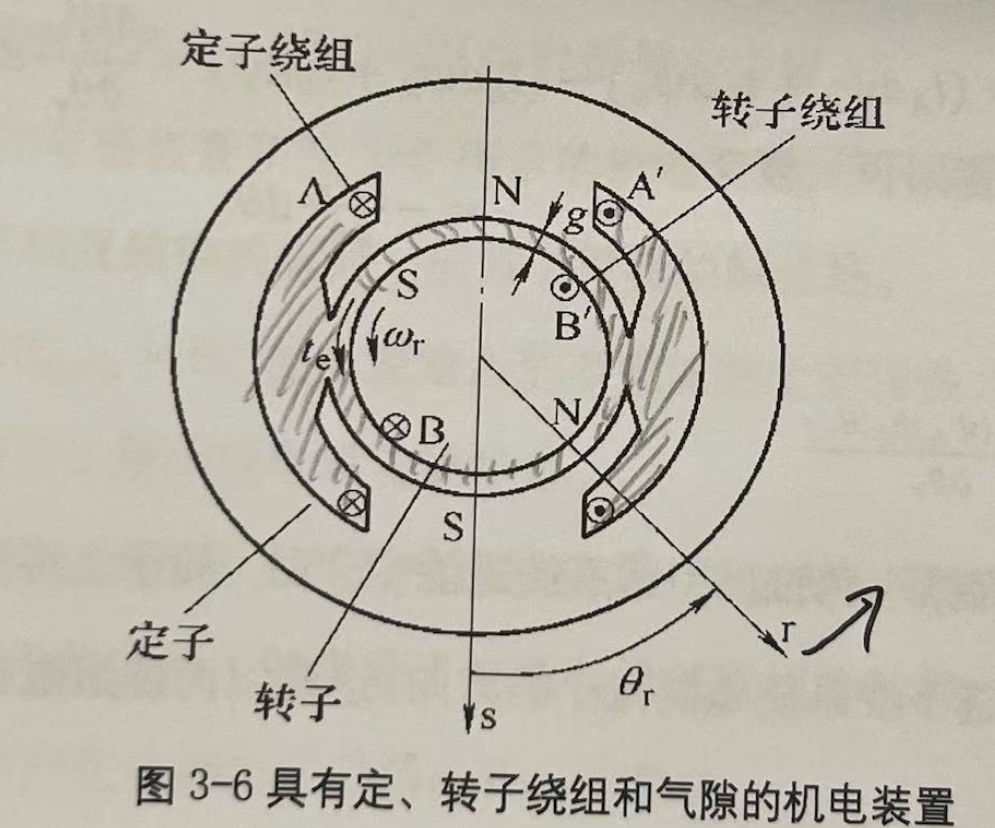
- 定转子之间气隙长度为 $g$ ,总气隙 $\delta = 2g$ ,忽略定、转子磁路的磁阻,则磁场能量全部存储在气隙中
- 线圈 A 匝数为 $N_A$ ,线圈 B 的匝数为 $N_B = N_A$
- 考虑图中的电流 $i_A$ 、 $i_B$ 的正方向,可以得到定子的磁场轴线 $s$ 和转子的磁场轴线 $r$ ,则 $\theta_r$ 为转子位置角
- 气隙均匀,故定子的励磁电感 $L_{mA}$ 和转子的励磁电感 $L_{mB}$ 均不变,因为匝数相等,则 $L_{mA}=L_{mB}$
- 两者互感 $L_{AB} = M_{AB,max} \cos\theta_r$
- 当线圈 A 、 B 轴线重合时,两者处于全耦合状态,两者之间互感达到最大值 $M_{AB,max}$ ,考虑线圈参数相同,则 $L_{mA}=L_{mB}=M_{AB,max}$
- 磁能的表达式 $W_{m}=W_{m} ( \psi_{A}, \psi_{B}, \theta_{r} )$
- 磁链和转子位置变化而引起能量变化(假设 $T$ 方向为逆时针)
- 磁能 $d W_{m}=\frac{\partial W_{m}} {\partial\psi_{A}} d \psi_{A}+\frac{\partial W_{m}} {\partial\psi_{B}} d \psi_{B}+\frac{\partial W_{m}} {\partial\theta_{r}} d \theta_{r}$
- 净电能 $dW_e = dW_m + dW_{\text{mech}} = dW_m + Td\theta_r$
- 机械能 $Td\theta_r = dW_e - dW_m= (i_A d\psi_A + i_B d\psi_B) - (i_A d\psi_A + i_B d\psi_B + \frac{\partial W_m}{\partial \theta_r} d\theta_r)$
- $Td\theta_r = -\frac{\partial W_m}{\partial \theta_r}d\theta_r$
- 最终得到转矩公式,$T = -\frac{\partial W_m(\psi_A, \psi_B, \theta_r)}{\partial \theta_r}|_{\psi = const}$
- 说明电磁转矩为系统磁能减小的方向,理解为系统磁能转化为机械能
- 同理可得另一个形式的转矩公式 $T= \frac{ \partial W_{m}^{ \prime} \left( i_{A},i_{B}, \theta_{r} \right)}{ \partial \theta_{r}}|_{i=const}$
- 磁共能 $W_m’=\frac{1}{2}L_Ai_A^2+\frac{1}{2}L_Bi_B^2+M_{AB,max} \cos\theta_ri_Ai_B$
- 则转矩 $T=-i_Ai_BM_{AB,max}\sin\theta_r$
- 若设转矩 $T$ 为顺时针方向,则 $T=i_Ai_BM_{AB,max}\sin\theta_r$
电机转矩的统一公式
电磁转矩生成的实质
电机的转矩包括励磁转矩和磁阻转矩,这两者共同构成电磁转矩

$T=i_Ai_BM_{AB,max} \sin\theta_r$
定子励磁磁场和转子磁场相互作用产生转矩——励磁转矩
直观解释:
- 转子磁场畸变了定子电流建立的气隙磁场
- 而气隙磁场倾向于不被畸变,故而产生了转矩
公式推导:
- 在设定转矩正方向为顺时针方向时,电机转矩公式如下( $M_{AB,max} = L_A = L_B$ )
$$
T=\frac{1} {L_{\mathrm{m B}}} ( L_{\mathrm{m B}} i_{B} ) ( L_{\mathrm{m A}} i_{A} ) , s i n , \theta_{r}=\frac{1} {L_{\mathrm{m B}}} \psi_{\mathrm{m B}} \psi_{\mathrm{m A}} , s i n , \theta_{r}
$$
举例说明:
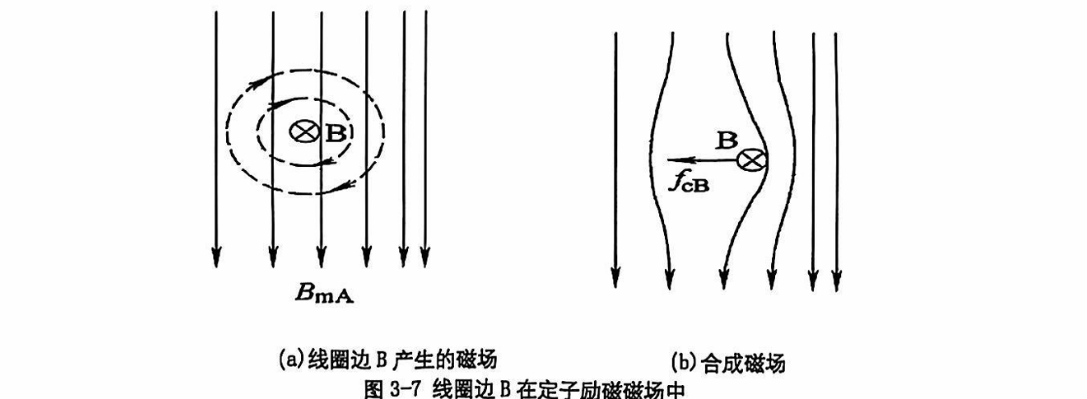
磁力线试图变直,故而对线圈的 B 边产生了向左的力
$$
T=\psi_{\mathrm{m A}} i_{B} , s i n , \theta_{r}
$$
转子无励磁但为凸极式,旋转时也会畸变气隙磁场——磁阻转矩
(说实话,这张图真难看)
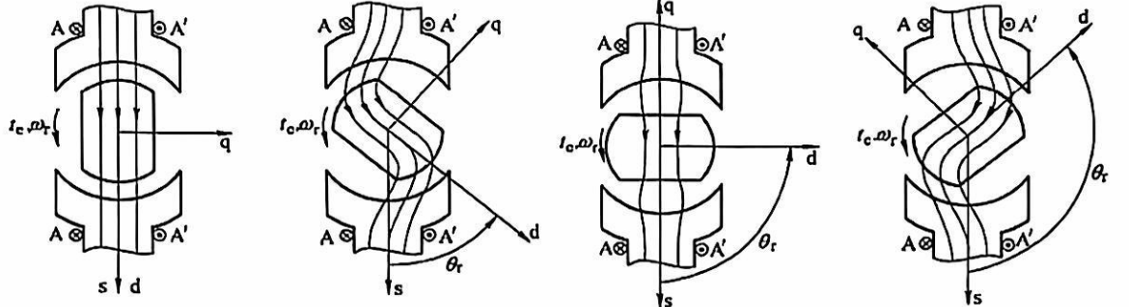
定子绕组自感在直轴电感 $L_d$ 和交轴电感 $L_q$ 之间变化,取基波分量( $L_d$ 直轴气隙小,磁阻小,电感大)
- $L_{A} \left( \theta_{r} \right)=L_{0}+ \Delta L \cos 2 \theta_{r}$
- $\left. \right. L_{0}= \frac{1}{2} \left( L_{d}+L_{q} \right), \Delta L= \frac{1}{2} \left( L_{d}-L_{q} \right)$
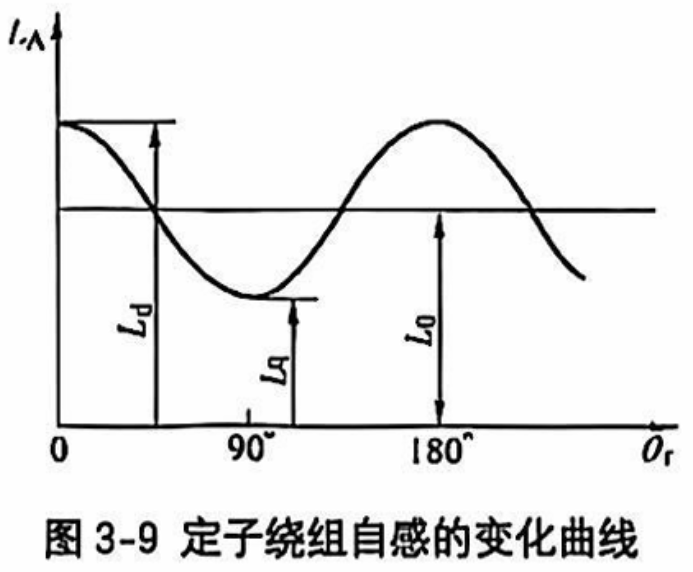
- $T=- \Delta Li_{A}^{2} \sin 2 \theta_{r}=- \frac{1}{2} \left( L_{d}-L_{q} \right) i_{A}^{2} \sin 2 \theta_{r}$ ,取逆时针为正方向时
电磁转矩总结
综上,取顺时针为正方向,则 $T=p(M_{AB,max}i_Bi_A\sin\theta_r+\frac{1}{2}\left( L_{d}-L_{q} \right) i_{A}^{2} \sin 2 \theta_{r})$
电机的数学模型
对位置的控制——>对电机速度的控制——>对电机转矩的控制——>定转子电流、磁链及其夹角
利用上述转化,将各种电机等效为 $p$ 对极的定子电流 $i_s$ 、转子电流为 $i_r$ 的电机进行研究控制
通过定子电流 $i_s$ 、转子电流为 $i_r$ 以及夹角 $\theta_r$ 来控制
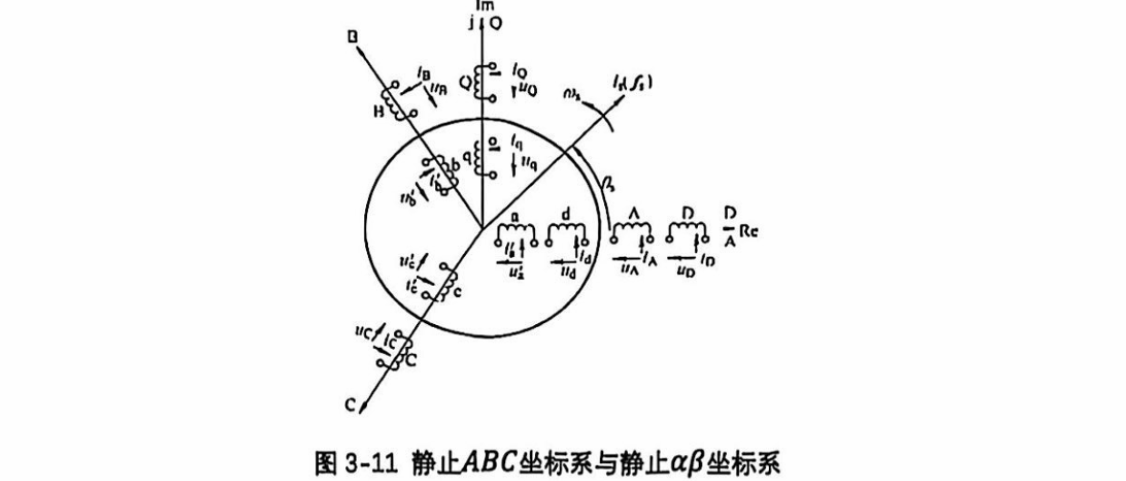
基于定子坐标系的三相感应电机数学模型(基于下图推导)
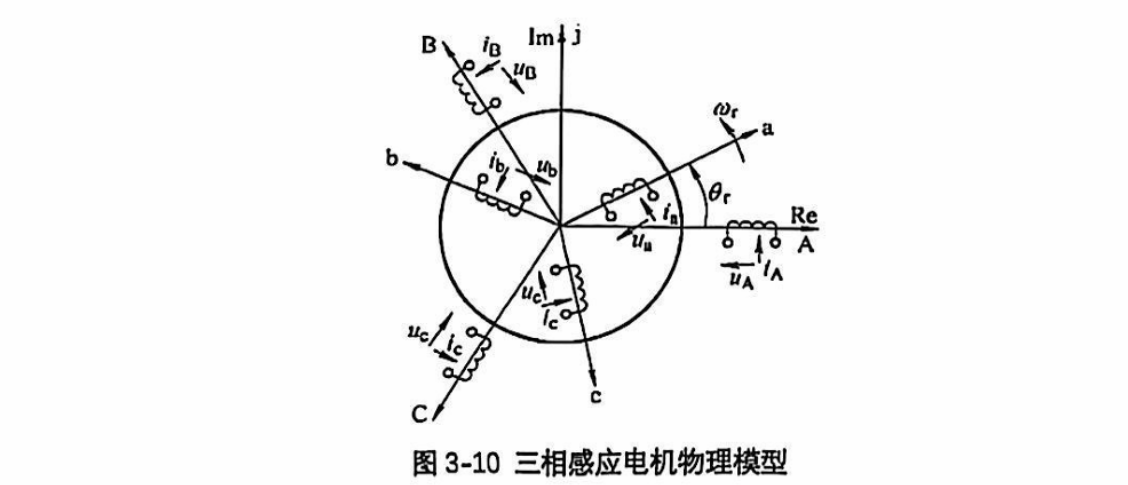
电压方程的推导,需要定转子的电压方程
- 定子的电压方程直接列写
- $\vec u_s=\vec i_s R_s +\frac{d\vec\psi_s}{dt}$
- 转子的电压方程需要通过夹角转化(求其中一相)
- $\vec{u_r^r}=R_{r} \vec{i_r^r}+ \frac{d {\vec\psi_r^r}}{dt}$ ,转子两端电压公式基于转子静止坐标系
- $\vec{u}{r}^{r} =\vec{u}{r} e^{-j\theta_r}$
- $\vec{i}{r}^{r} = \vec {i}{r} e^{-j\theta_r}$
- $\vec{\psi}{r}^{r} ={\vec \psi}{r} e^{-j\theta_r}$
- 则 $\vec{u}{r}=R{r} \vec{i}{r} + \frac{d {\vec\psi_r}}{dt} - j\omega_r {\vec\psi}{r}$ (在定子静止坐标系)其中转子转速 $\omega_r = \frac{d\theta_r}{dt}$
- 转子磁链的极坐标表示 $\vec\psi_{r}=\psi_{r}e^{j\rho_r}$
- 则 $\vec{u}{r}=R{r} \vec{i}{r} + \frac{d {\psi_r}}{dt} e^{j\rho_r} + j(\omega_s - \omega_r)\vec{\psi}{r}=R_{r} {i}{r} + \frac{d {\psi_r}}{dt}e^{j\rho_r} + js\omega_s\vec{\psi}{r}$ ,其中定子转速 $\omega_s=\frac{d\rho_r}{dt}$
- 考虑 $P\vec\psi_r$ 为仅对 $\vec\psi_r$ 的幅值微分,即 $P\vec\psi_r= \frac{d {\psi_r}}{dt} e^{j\rho_r}$
磁链方程(考虑自感互感)
- $\vec\psi_s = L_s\vec i_s+L_m\vec i_r$
- $\vec \psi_r = L_r\vec i_r+L_m\vec i_s$
转矩方程(上一节的结论,包括励磁转矩和磁阻转矩)
- $T_{e}=p \left[ L_{m}i_{r} \times i_{s}+ \frac{1}{2} \left( L_{d}-L_{q} \right) i_{s}^{2} \sin 2 \theta_{r} \right]$
动力学方程(上一章结论,牛顿旋转方程推导而来)
- $T_{e}-T_{L}= \frac{GD^{2}}{375} \times \frac{dn}{dt}$
转速方程
- $n = \frac{60}{2\pi}\omega_r = \frac{60}{2\pi}\frac{d\theta}{dt}$
坐标转换
(看,我不骗人,简单的图我都自己画)

上述求得的三相感应电机数学模型参数多,减少参数(便于建模?)
坐标变换的原则(希望变换前后能够等效)
- 磁动势不变
- 功率不变
思考变换前磁动势的大小?
- 错误观点1,只考虑了时间相位,没有考虑空间
- $i_a+i_b+ i_c=0$ ,在只考虑时间时是成立的
- 如得到 $\vec f = N\vec i_a + N \vec i_b +N\vec i_c=0$ 则是错误的
- 因为磁动势是空间分布的
- 正确观点,磁动势是旋转矢量
克拉克变换Clarke变换
电机的数学模型
他励直流电动机的数学模型
异步电机的数学模型
同步电动机的数学模型
闭环电机控制系统
传统的闭环电机控制
- 单闭环速度控制*
- 双闭环速度、电流控制**
单闭环他励直流电动机控制系统
- 有静差控制系统,比例控制
- 无静差控制系统,比例积分控制
有静差他励直流电动机控制系统是单纯由被调量负反馈组成的按比例控制的单闭环系统
控制系统的介绍
(这是我觉得本书最丑的一张图)
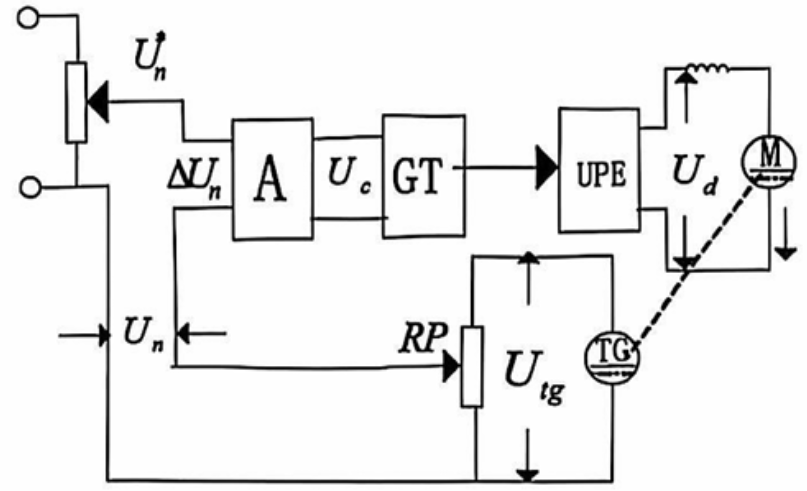
- 测速发电机 TG 测量电机实际转速,输出一个电压信号 $U_{tg}$ ,该电压信号正比于电机的转速 $n$
- $U_{tg} =C_n n$ ,其中 $C_n$ 为侧速发电机的电动势常数
- $U_{tg}$ 通过信号处理后得到反馈信号 $U_n$
- $U_n=K_fU_{tg}=\alpha n$ ,其中 $K_f$ 为电位器分压系数, $\alpha$ 为转速反馈系数, $\alpha=K_fC_n$
- $U_n$ 与给定的控制转速的电压信号 $U_n^*$ 做差,再经放大器 A 放大后,产生触发器 GT 的控制电压 $U_c$
- $\Delta U_n=U_n^*-U_n$
- $U_c=K_p\Delta U_n$ ,其中 $K_p$ 为放大器 A 放大倍数
- 触发器 GT 的输出给到整流器,进而改变直流电机的电枢电压,实现对电机转速 $n$ 的控制
- $U_{d0}=K_sU_c$ , $K_s$ 是整流器和触发器总的放大倍数
- 即 $U_{d0}=K_pK_s|U_n^*-\alpha n|$ ,此处只考虑 $U_n^ > \alpha n$ 的情况*
- 故 $U_{d0}=K_pK_s(U_n^*-\alpha n)$
- UPE主功率单元 Unit of Power Electronics
- GT触发电路 Gate Trigger
反馈控制过程
- 当电机轴上的负载增大时,电枢电流 $I_a$ 随之增大(为什么?)
- 电枢回路电阻上的电压降增加,速度降低的绝对值 $\Delta n=\frac{I_aR_\sum}{C_e\Phi}$增加
- 电机转速减小, $U_n$ 减小, $\Delta U_n$ 增大,触发器控制电压 $U_c$ 增大,整流器输出电压 $U_{d0}$ 增大
- 电机转速 $n = \frac{U_{d0}-I_aR_\sum}{C_e\Phi}$ 增加
- 负载减小时分析过程同理
- 总结,负反馈闭环控制可以使得电机的转速尽可能保持不变
稳态性能(这部分均为自控知识,可以从上述的过程直接推导出以下稳态性能公式,但是还是根据下面的方块图来直接写更好,如果你不知道,说明需要补充自控知识)
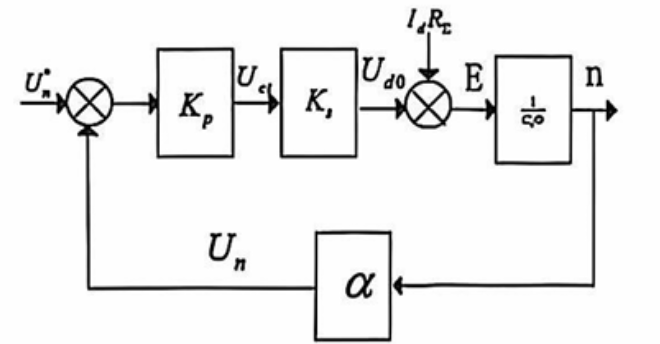
- 闭环机械特性 $n=\frac{K_pK_s}{C_e\Phi(1+K)}U_n^*-\frac{1}{C_e\Phi(1+K)}I_dR_\sum=n_{0close}-\Delta n_{close}$
- 其中 $K=\frac{K_pK_s\alpha}{C_e\Phi}$为开环放大倍数
- 开环机械特性 $n=\frac{K_pK_s}{C_e\Phi}U_n^*-\frac{1}{C_e\Phi}I_dR_\sum=n_{0open}-\Delta n_{open}$
- 其中 $n_0$ 均表示理想空载转速, $\Delta n$ 均为速降
得出如下结论
- 闭环系统的稳态特性比开环系统的机械特性硬得多
- 在同样扰动下,闭环的速降只有开环速降的 $\frac{1}{1+K}$
- 当 $K$ 值较大时,闭环系统得静差率较小
- 同一理想转速下,闭环的静差率只有开环静差率的 $\frac{1}{1+K}$
- 当生产工艺要求得静差率一致时,在同一额定转速下,闭环系统的调速范围是开环系统的 $K+1$ 倍
- 调速范围 $D_{open}=\frac{n_Ns_D}{\Delta n_{open}(1-s_D)}$
- 闭环系统具有更好的服从给定、抑制扰动的性质
- 系统的精度依赖于给定信号和反馈检测环节的精度
无静差他励直流电动机控制系统是按比例积分控制的系统
比例调节在无静差时输出为 0 ,故无作用
双闭环他励直流电动机控制系统
三相电机驱动系统的硬件设计
注
参考上海交通大学电机控制技术课程组教材
