滑动窗口

就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

回溯算法

回溯=穷举

概述

递归和回溯的区别？

  • 递归是一种编程技术，其中一个函数通过调用自身来解决问题，通常将大问题分解为更小的子问题，直到子问题可以直接求解。
  • 回溯是一种算法设计技术，通过试探和撤销的方式，系统地搜索所有可能的解空间，找到满足条件的解。可以看作是递归的一种特殊形式，但在递归的基础上增加了状态的恢复（撤销操作）。

回溯解决的问题

  • 组合问题：在 N 个数中按一定规则找出 k 个数
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个 N 个数的集合里有多少符合条件的子集
  • 排列问题： N 个数按一定规则全排列，有多少种排列方式
  • 棋盘问题： N 皇后，解数独

如何理解回溯的结构？树！！！

  • 递归的深度为树的深度
  • 每层递归搜索的次数为树的分叉数

回溯法三部曲—— for 横向遍历、递归竖向遍历

  • 递归函数的返回值及其参数
  • 回溯函数终止条件
  • 回溯搜索的遍历过程
1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) { // 搜索
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合问题

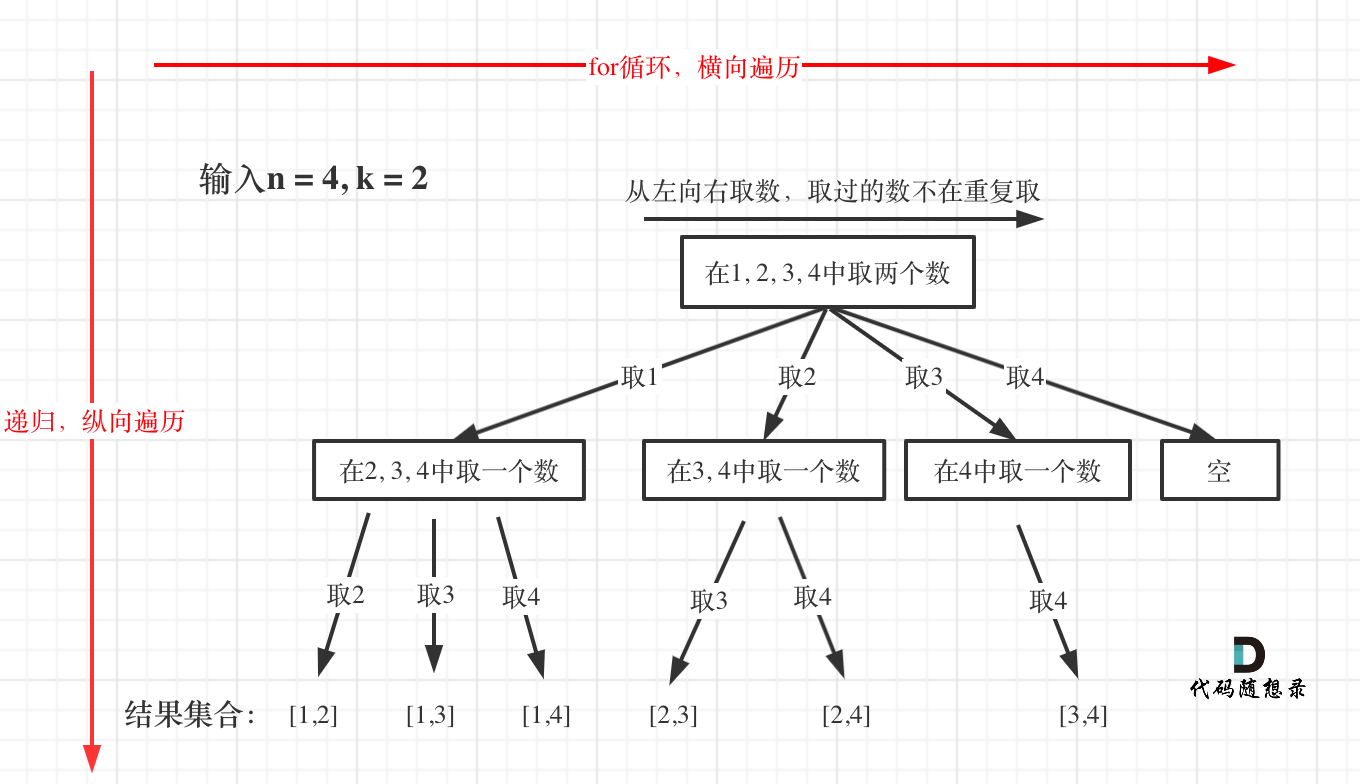
以题目举例：给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

1 为什么组合问题需要回溯法？
依次选择组合中的数直到选出 k 个，组合中的第 i 个数的选择需要枚举出可以用的数，这个时候就需要 for 循环嵌套，一方面，嵌套次数多，代码写成依托；此外如果在运行之前不知道循环嵌套的层数，写不出来代码。

故采用回溯的方法来解决问题

  • 每次递归都嵌套一次 for 循环
  • 递归深度增加表示选择的数的位置变大

2 for 循环的优化？
在 for 循环中，可以根据已知知识来提早结束循环
比如还要选择 x 个数，但是剩余的数只有 y < x 个，就可以直接结束了，后面再递归也是浪费时间

3 如何去重？
树层去重：同一层的去重，需要数组先排序，然后再判断当前元素是否与上一个元素是否一致；为什么可以呢？因为上一个元素肯定再这个元素出来之前就已经作为当前位置的元素递归过

4 组合问题的抽象（如下图）

image-20250503212215189

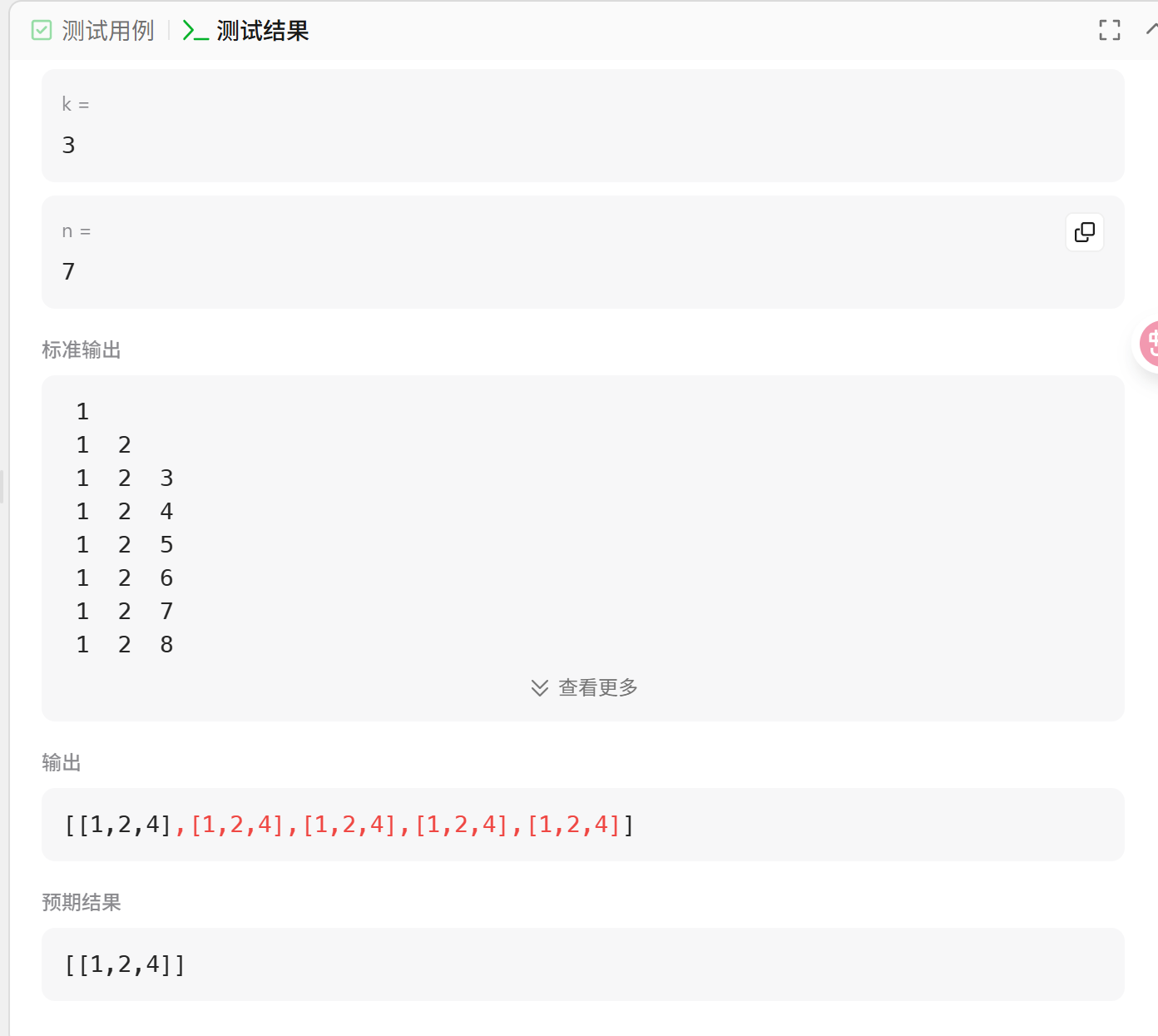
5 常见错误，下面的方法乍一看也可以递归呀，但为什么就是错呢？

  • 每次加入元素，先直接加入 cur_num 导致，递归开始的元素是无法搜索的，也就是说：将 1 作为调用的起点，之后的每次递归的首数字都是 1
  • 此外，由于每次是在加入当前元素的下一次调用时进行判断，正常情况下，没有问题，但是由于每次加入的是当前的 cur_num ，递归到下一层时，不管是哪一个元素，只要在最开始一步满足条件，就加入了答案，造成很多重复
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> cur;
    int sum = 0;
    void backtracking(int k, int n, int cur_num) {
        if (cur.size() == k && sum == n) {
            ans.push_back(cur);
            return;
        } else if (cur.size() == k) {
            return;
        }
        cur.push_back(cur_num);
        sum += cur_num;
        for (int i = 0; i < cur.size(); i++) {
            cout << " " << cur[i] << " ";
        }
        cout << endl;
        for (int i = cur_num + 1; i <= 9 - k + cur.size(); i++) {
            backtracking(k, n, i);
        }
        sum -= cur_num;
        cur.pop_back();
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        backtracking(k, n, 1);
        return ans;
    }
};
image-20250503212415426

切割问题

求解切割问题时，要找到切割的位置，切割之后不能继续在原位置继续切，那就永远递归了
切割时，要明确切割后的子串，子串的起始点、结束点都要弄明白

单调栈

对于一个数组，我们想要获取每个元素之后第一个比它大的元素的位置，就可以用单调栈

1 为什么呢？
举例说明一下，数组的第一个数为 nums[0] ，我们现在目的是要寻找第一个大于 nums[0] 的数。
我们开启一个循环，开始遍历，遇到比 nums[0] 小的元素我们都跳过，最终如果存在比 nums[0] 大的元素，我们一定可以找到。假设1：现在不妨先假设存在，则假设找到的元素为 nums[k]。
在这个过程中，我们浪费了一些已知条件。

2 什么条件呢？
在区间 (0, k) 的元素都是小于 nums[0] 和 nums[k] 的

3 如何利用这个条件？
假设2：先不妨再做出一个假设，(0, k) 区间只有一个数，这个时候我们毫无疑问可以确定这个数的后一个比他大的就是 nums[k] ，想要在代码中实现这一点，我们就需要将这个元素保存起来，之后才能比较。
现在存放数的容器里面应该是 [nums[0], nums[1]] ，当 nums[2] 来的时候，它是大于 nums[1] 的，可以先将 nums[1] 移出容器了，因为它的下一个最大已经确定好了。当到 nums[0] 时，只能确定两者的大小关系，但是不能确定 index ，所以，存在元素到容器里面时，采用存储下标的方法，这样就可以确定位置关系了，并且可以根据索引确定元素值。

4 以上结束之后，我们逐步放宽做出的假设（以下部分提到的值是元素实际的值，而不是索引，索引只在需要计算位置关系时才考虑）
先放宽假设2，此时内部有多个元素。根据前面的推导，我们在确定了一个元素的下一个最大之后，就会将其移出容器，所以，容器中存在的元素的值应该是递减的（注：这个是由于上面的推导演化而来，不是凭空产生）。现在新来的元素，如果比容器里最后的元素大，则需要移出元素。从而保证容器内部的递减。
再放宽假设1，最后容器中还存在元素，说明没有找到下一个最大，则全部设为0

至此，推导过程结束。容器选择：相信看到这，你会毫不犹豫选择栈，因为只需要管理栈顶。
总结
我们想要获取的是第一个比他大的
单调栈内部维护的是递减
当来了一个数，大于栈顶元素的值，说明找到了第一个比他大的元素，按此方法，问题则解决了

哈希表

通过 key 来访问 value

哈希表理论基础

1 什么是哈希表？
能够直接通过 key 来访问 value

2 什么时候用到哈希表？

  • 快速判断一个元素是否存在

3 什么是哈希函数？
通过哈希函数将 key 映射到哈希表的位置

4 哈希碰撞
当两个及以上 key 映射到哈希表同一个位置——称为哈希碰撞
解决方法

  • 拉链法，后来的元素接在当前位置的链表尾部
  • 线性探测法，后来的元素递增位置，直到找到空位置

5 常见的三种哈希结构

  • 数组
  • set
    • std::set
    • std::multiset
    • std::unordered_set，基于哈希表
  • map
    • std::map
    • std::multimap
    • std::unordered_map，基于哈希表

双指针法

KMP

KMP算法解决的问题：在文本串 S 中寻找模式串 P ，如果找到，返回首字母的位置

KMP的思想，当模式串 P 和文本串 S 有一部分匹配时，可以通过模式串的已知条件确认文本串目前的状态

以模式串为 ABABC 、文本串为 ABABDABABC 为例，来说明上述思想
先逐个匹配，前四个索引的 ABAB 是匹配的，接下来遇到的 C 和 D 不匹配

暴力算法遇到这个情况，需要从文本串的第二个字符 B 开始重新比较一遍模式串和文本串是否相同；但其实是否需要这样呢？还有什么条件没有用到？上述提到的，模式串中记录到的文本串的信息。如何利用这个信息就是KMP算法的关键。

KMP是怎么利用信息的？因为 ABAB 这个是已经匹配的，所以确定文本串的字符 D 前两个字符为 AB ，这部分与模式串的开头两个字符 AB 是匹配的，则这部分不需要再比较（我们人肉眼可以知道，但是如何让程序知道呢，如何记载？next数组）

此处我们先假设求到了next数组，直接使用，还是接着上面的例子说明如何使用next数组
ABAB 中已经匹配好了 AB 这部分的字符，所以现在我们应该可以直接比较模式串的第三个字符 A 与文本串的字符 D ，这个过程中，next数组要告诉我们的就是如何把模式串要比较的字符从第五个字符 C 移动到第三个字符 A

next数组怎么求？
具体步骤
设模式串为 P，长度为 m：

  1. 初始化：
    • 令 next[0] = 0，因为第一个字符之前没有任何前后缀
  2. 维护两个指针：
    • i 指向模式串当前要处理的字符
    • j 表示当前字符的最长相等前后缀长度
  3. 更新规则：
    • 若 P[i] == P[j]：
      • 匹配成功，j 向右移动，增加前后缀长度
      • 令 next[i] = j + 1
    • 若 P[i] != P[j]：
      • 匹配失败，j 根据 next[j - 1] 回
      • 重复比较，直到找到匹配位置或 j == 0
    • 如果最终没有找到匹配，令 next[i] = 0
  4. 循环直到处理完所有字符。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
i = 0: P[0] = 'A'
  next[0] = 0 (第一个字符没有前后缀)

i = 1: P[1] = 'B'
  P[1] != P[0]，next[1] = 0 (无相等前后缀)

i = 2: P[2] = 'A'
  P[2] == P[0]，next[2] = 1 (前缀 "A" == 后缀 "A")

i = 3: P[3] = 'B'
  P[3] == P[1]，next[3] = 2 (前缀 "AB" == 后缀 "AB")

i = 4: P[4] = 'C'
  P[4] != P[2]，回退 j = next[1] = 0
  P[4] != P[0]，next[4] = 0 (无相等前后缀)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <iostream>
#include <vector>
#include <string>

using namespace std;
// 计算模式串的 next 数组
vector<int> computeNext(const string &pattern) {
    int m = pattern.length();
    vector<int> next(m, 0);
    int j = 0; // 前缀长度

    for (int i = 1; i < m; ++i) {
        while (j > 0 && pattern[i] != pattern[j]) {
            j = next[j - 1]; // 回退
        }
        if (pattern[i] == pattern[j]) {
            ++j; // 匹配增加前缀长度
        }
        next[i] = j;
    }

    return next;
}

// KMP 搜索算法
int kmpSearch(const string &text, const string &pattern) {
    int n = text.length();
    int m = pattern.length();
    vector<int> next = computeNext(pattern);

    int j = 0; // 模式串指针
    for (int i = 0; i < n; ++i) {
        while (j > 0 && text[i] != pattern[j]) {
            j = next[j - 1]; // 回退
        }
        if (text[i] == pattern[j]) {
            ++j; // 匹配增加
        }
        if (j == m) {
            return i - m + 1; // 匹配成功，返回起始位置
        }
    }

    return -1; // 未找到匹配
}

int main() {
    string text = "ABABDABABC";
    string pattern = "ABABC";

    int result = kmpSearch(text, pattern);
    if (result != -1) {
        cout << "Pattern found at index: " << result << endl;
    } else {
        cout << "Pattern not found in the text." << endl;
    }

    return 0;
}